DESCRIPCIÓN:
Aquí se recogen los apuntes del curso 2020-2021 de cada uno de los temas de la asignatura; organigramas, interpolación de Lagrange, interpolación de Newton y mínimos cuadrados.
JUSTIFICACIÓN:
Para poder aprobar la asignatura son fundamentales unos apuntes claros y concisos que nos permitan entender todos los temas, y, una vez entendidos, poder practicar con diversos ejercicios. Además, unos apuntes llamativos visualmente hablando, son muy útiles en los días previos al examen para repasar y tenerlo todo claro.
RECOMENDACIÓN:
Es importante mirar bien todos los apuntes antes de ponerse a hacer ejercicios como un loco, ya que hay ejercicios muy diferentes, pero si se entienden bien los conceptos se pueden deducir o intuir las resoluciones de los mismos.
CONTROL DE CALIDAD:
Estos apuntes son una fusión de los apuntes de cada uno de los miembros del grupo, y dichos apuntes ha sido tomados en las clases siguiendo las pautas del profesor.
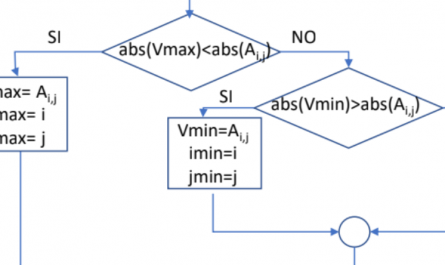
ORGANIGRAMAS:
La asignatura puede un poco frustrante al inicio, ya que es complicado entender el tema de organigramas por lo novedoso que resulta. Además, este tema es el más importante de todos ya que los organigramas aparecerán en los temas siguientes, puesto que son la base de toda la algoritmia. Desde sumatorios y productos hasta qué tipos de bucles hay y cuál es la función de cada uno de ellos, en este link encontrarás los apuntes que te ayudarán a entender todos estos conceptos.
INTERPOLACIÓN:
El concepto de interpolación es difícil de entender también, por eso estos apuntes te vendrán de maravilla, por no hablar de que es un apartado denso en el que se explican muchas cosas por lo que debes tener unos apuntes que te ayuden a no perderte en el bloque +de interpolación.
MÍNIMOS CUADRADOS
Este último tema es mas sencillo, aunque hay muchas fórmulas y si no tienes unos apuntes claros y breves puedes perderte. Aquí te dejamos los apuntes de este tema.